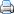The Black Keys

Sharps and Flats

Naming Rules for Singers

Sol

Sil

Sal

Sol

The first row has names when sharps appear. The second row has names when flats appear.

THE DIFFERENT SCALES.

We learnt from the diagram of the Chromatic Scale, that it has 12 steps which are numbered 1 to 12 and only 7 steps are used in a given tune. When we start our selection from key no. 1 of the Chromatic Scale, which is called C, we get the selection of the 7 notes as follows:

1	2	3	4	5	6	7	8	9	10	11	12	1
C		D		E	F		G		A		B	C
Do		Re		Mi	Fa		Sol		La		Si	Do

When shifting the pitch upwards or downwards we start our scale of seven sounds from a different step of the Chromatic Scale. If we start on step 8 which is G, we get F# and if we start on 6 which is F, we get B flat, by retaining the structure of tones and semitones.

8	9	10	11	12	1	2	3	4	5	6	7	8
Do		Re		Mi	Fa		Sol		La		Si	Do
G		A		B	C		D		E		F#	G

8 9 10 11 12 1 2 3 4 5 6 7 8

G A B C D E F# G

DO RE MI FA SOL LA SI DO

6 7 8 9 10 11 12 1 2 3 4 5 6

F G A Bb C D E F

DO RE MI FA SOL LA SI DO

Note that we can not call the step 11 as A# as we are using the name A for MI. Since step 12 is unused, we call 11 as B flat.

As a general principle, when we raise the pitch, we get sharps, and when we lower it, we get flats.

As the pitch is raised from Chromatic Step 1 to Step 8, we get the 7^th step as the sharp. In the same way, when we rise from the 8^th step, another 8 steps, we reach the 3^rd step (because 12 is followed by 1), and the 2^nd step is used instead of 1 and we get C#. In this case, the previous F# is retained. This new sharp is the “Si” or 7^th note of the scale.

8 9 10 11 12 1 2 3 (the 8^th step above)

3 4 5 6 7 8 9 10 11 12 1 2 3

D E F# G A B C# D

DO RE MI FA SOL LA SI DO

THE FLAT SCALES:

Going 8 steps down at a time on the Chromatic Ladder, we get an additional flat each time:

1 12 11 10 9 8 7 6

Starting on step 6 we saw above that we get B flat - or 1 flat scale, with F as the starting note of the Scale. Now let us go downwards from step 6:

6 5 4 3 2 1 12 11

11 12 1 2 3 4 5 6 7 8 9 10 11

Bb C D Eb F G A Bb

The 4^th note of the new scale is the newest flat, besides the starting note. Hence this is a 2 flat scale. We give below two tables one for the sharp scales and the other for the flat scales. The scales are known by the first key name of the scale: F scale, G scale etc.

THE SHARP SCALES.
C	All white keys.
G	F#
D	F#	C#
A	F#	C#	G#
E	F#	C#	G#	D#
B	F#	C#	G#	D#	A#
F#	F#	C#	G#	D#	A#	E#(F KEY)*
C#	F#	C#	G#	D#	A#	E#	B# (C KEY)*

For theoretical reasons, we have to call these white keys a s sharp keys since the white key is already modified in the scale, and we can not have the same name repeated.

THE FLAT SCALES
C	All white keys.
F	Bb
Bb	Bb	Eb
Eb	Bb	Eb	Ab
Ab	Bb	Eb	Ab	Db
Db	Bb	Eb	Ab	Db	Gb
Gb	Bb	Eb	Ab	Db	Gb	Cb*
Cb	Bb	Eb	Ab	Db	Gb	Cb	Fb*

HARMONIC NAMES OF THE SCALE:

· Key Note, or Tonic: the starting note of the scale.

· Super Tonic – the second note of the scale.

· Mediant – the third note of the scale

· Sub dominant – the fourth note of the scale

· Dominant – the fifth note of the scale

· Sub Mediant – the sixth note of the scale

· Leading Note – the seventh note of the scale.

chords – the foundation of harmony

Sound distance between notes

A chord is formed by taking two alternate named keys above any note. Thus chord on the Tonic of a natural scale would be: C E G. On the other hand the Tonic chord of F scale would be: F A C. The tonic chord of G scale would be G B D. The tonic chord of D scale would be D F# A. The F# forms the part of the scale, and is the next alternate name after D.

Similarly we can form chords on all the notes of the scale, in every scale.

· All Tonic, Dominant and Subdominant chords are called Primary Chords.

· The Secondary Chords are those on: The Supertonic, Mediant and Submediant.

· The chord on the Leading Note is called : The Diminished Chord.

the three primary chords of the c scale”

1 2 3 4 5 6 7 8

C E G The Tonic Chord

8 9 10 11 12 1 2 3

G B D The Dominant Chord

6 7 8 9 10 11 12 1

F A C The Subdominant Chord

the distances or intervals BETWEEN 2 notes:

the thirds

There are two ways at looking at the distances. One the diatonic way, that is to say, what you see on the stave. Practically it works out, to be the serial sequence of the alphabetic name: If we take A as the first name, and B is the second name, B is at a distance of a 2^nd from A. Same way, C is at a distance of 3^rd from A, and D is at a distance of 4^th from A.

These distances vary when seen on the chromatic scale.

In the above diagrams of the three primary chords: the three notes of the chord are at a distance of a 3^rd according to the diatonic order. However, when you see it in comparison with the chromatic scale, you will note that the distances are not the same. The distance of the first two notes is more than that of the latter two notes. Hence we place qualifiers with the interval in the diatonic order. The first kind will be called Major thirds, and the latter will be called Minor thirds.

Major thirds have five chromatic keys between the two notes, and the Minor thirds have four chromatic keys between these two notes forming thirds.

the fifths:

From the above example, note the distance between C and G, it is a fifth. Every chord therefore is made up of a third and a fifth above the root of the chord. In the above examples, every fifth is equal in distance: i.e. they have 8 chromatic keys between the two notes. Such fifths are called PERFECT FIFTHS

MAJOR CHORDS: These are made up of a Major third and a perfect fifth above the root.

MINOR CHORDS: These are made up of a Minor third and a perfect fifth above the root.

3 4 5 6 7 8 9 10

D F A - The supertonic chord

5 6 7 8 9 10 11 12

E G B – The Mediant chord

10 11 12 1 2 3 4 5

A C E – The submediant chord.

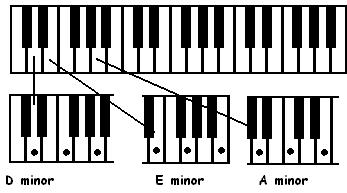
The chord names are generic and can be applied to all scales, however their proper names are given by using the name of the root: D minor, E Minor and A minor or in short form Dm Em and Am.

In the case of major chords, only the root name is given in the Capital type of the alphabet. C major is written C, F major is written F, E major will be E etc.

the diminished chord

12 1 2 3 4 5 6

B D F – Chord on the Leading Note.

Note that in this case, we have a minor third above the root, and the fifth has 1 semitone less than a perfect fifth. It is called the Diminished fifth. Looking at it in another way: both the thirds are minor.

chord of the dominant seventh

8 9 10 11 12 1 2 3 4 5 6 7

G B D F

· There are three thirds placed one above the other.

· The third above the root is Major

· Fifth above the root is Perfect

· Seventh above the root is “minor”

· (A major seventh has 12 chromatic keys between the first and seventh name).

· C to Bb is a minor seventh. G to F# is a major seventh.

Looking at it from another angle: the three thirds are: Major, minor, major.

Another way: Dominant seventh is a mixture of G and the B chord (Dominant and the Leading Note chords).

CONCEPT OF A SCALE

A DIATONIC SCALE is made of 7 notes:

A B C D E F G

· the eighth note is repetition of the first:

· it is named diatonic because the notes ascend through the degrees of the stave. Each degree is reserved for one name.

We can start the scale on any name and end it on the 8th note which has the same name as the first:

B C D E F G A B

C D E F G A B C

The distance from one note name to the next note name is not equal. See the keyboard:

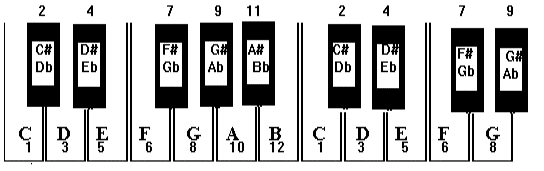
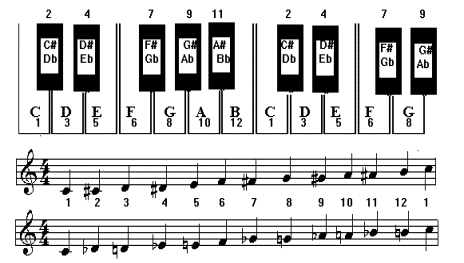
The black key between the white keys C and D has 2 names: C# and Db - i.e.

black key to the right of C = C#;

The distance between a white and a black key, immediately to the left or right of it is called a SEMITONE or HALF STEP.

· The semitone is the smallest distance (interval) between any two sounds on the chromatic scale.

When there are two white keys without a black key in between them, like E - F, and B - C, these too are SEMITONES. In the above keyboard diagram, the different keys are numbered 1 to 12. A pair of adjacent numbers, form a semitone. 1 to 2; 4 to 5; 5 to 6 etc.

A Chromatic Semitone A diatonic Semitone

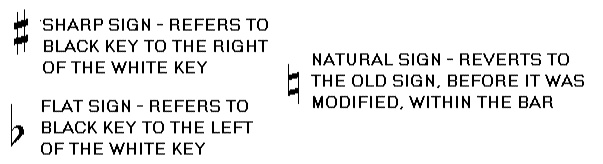
When the notes forming the semitone are written on the stave, you will either find them on the same degree of the stave, or on adjacent degrees. If they are on the same degree (the two notes have the same name) the semitone is called a CHROMATIC SEMITONE (CST). If they are on adjacent degrees (line/space) of a stave (they have two different names) they form a DIATONIC SEMITONE (DST)

A tone, or whole step is made up of one chromatic and one diatonic semitone.

The two notes forming a tone have to be on adjacent degrees of the stave and have adjacent names. Thus physically key 5 to 7 (of the 12 note scale) forms a tone, and if you call 5 as E, then 7 can not bear the name G flat, but has to bear the name F sharp, because E and F are adjacent names.

THE CHROMATIC SCALE.

The keyboard chart including names of black keys on p. 33 has numbers 1 - 12 for the keys inclusive of black keys. These refer to the steps of the chromatic scale.

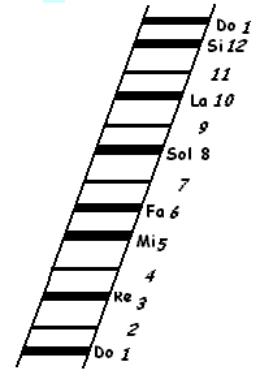It is the mother of all other scales. The word SCALE comes from the Latin word: SCALA which means a ladder.

The Chromatic Scale is shown as a ladder with 12 steps. Of these 5 steps are generally not used - these are: 2, 4, 7, 9 and 11, if a diatonic scale starts on step 1. On a keyboard, these are black keys.

The White Keys are:

Thus C = 1. D=3. E=5. F=6

G=8. A=10 and B=12

THE DIFFERENT SCALES.

We often need to raise or lower the pitch of a tune to suit the range of individual singers and the Organist has to use some black keys as compensation.

On page 32, we had seen exercises where we used the F sharp and B flat keys, and the singers renamed the notes. In the following exercises, we will use scales which have been moved up or down from its Natural position.

The most common scale we use, is called the Major Scale, and the steps are as selected in the picture of the Chromatic Scale, where the first two steps are a tone apart, followed by a step which is a semitone apart. Then 3 tones follow in succession and end with a semitone, leading to the upper pitch of the starting note, which is also called the Key Note, or the Tonic.

If you examine the scale closely, you will note that the first four notes and the last four notes are mirror copies. They are 2 tones and 1/2 tone and are called Tetrachords. The first four notes are the Lower Tetrachord and the upper four are the Upper Tetrachord. The tone between the two, is called the Tone of Disjunction.

For evaluating the different transposed scales, we make the upper tetrachord of a given scale, as the lower tetrachord of the new one, and the seventh note has to be given a sharp.

Thus, the Upper tetrachord of the Natural (C Scale) is G A B C. The new scale thus starts on G (Key Note), and the upper tetrachord becomes: D E F G. (According to rule, F needs to be sharpened.) Thus we get the 1 sharp scale, which is called the G scale. Generally the sharp is written on the 5^th line immediately after the Clef.

In the above diagram we see that the upper tetrachord of the G scale is D E F# G, and the D scale starts with this as the lower tetrachord, and has A B C# D as the upper tetrachord, and is the he new D scale. Similarly, the next one is the A scale.

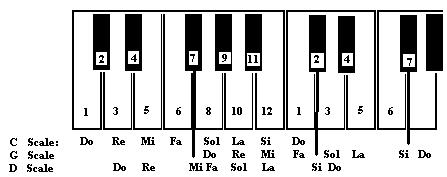
As for the singers, transposition means, moving the Do Re Mi, up or down the sound range. In the case of G scale, they call G as the Do, and rename all the other notes accordingly. In the case of D scale, D becomes Do, etc.

As a general principle, if we raise the pitch upwards by 8 chromatic steps, we always use the step before the 8th step as the note Si. As in the case of G scale, we raised the pitch to G which is step 8 of the chromatic scale, and used step 7 as our Si, which is F sharp. With each rising, we retain the older sharps.

Let us now see what happens if we do the reverse. Instead of taking the upper tetrachord to start a scale, we use the Lower tetrachord as the upper one of a new scale. In this experiment, we will see that we get the flat scales:

C D E F G A B C

F G A B C D E F

Now you notice that the lower tetrachord starting with F has 3 tones. In order to make the third interval a semitone, we can not use A#, as then the interval between G and A# will be more than 1 tone. You have to lower the B by a semitone, and we will get a bonus: we get the Tone of Disjunction..

If we move downwards to the 8^th step, we reach F. The first and last notes are having the same name thus we count only the new flat as the additional flat which is the fourth name from the starting name. From F if we move 8 chrromatic.steps downwards, we come to Bflat and the scale starting on this note has Bflat and the new E flat note. In the same way, we have the other flat scales, by moving downwards. Sharp scales are obtained by rising upwards 8 chromatic steps each time. The following table shows the starting note, and the accidentals (Sharp or flats)

SHARP SCALES

All White Keys

Tonic

Notes modified by accidentals.

E# (F KEY)*

B#(C KEY)*

* For technical reasons, these keys are named this way. Else we will have two keys with the same name in the stave. One with a sharp, the other without.

FLAT SCALES

All white keys.

Cb(B KEY)

Fb(E KEY)

Always the accidentals are placed at the beginning of the stave, immediately after the clef which tells you that the scale is a transposed one. If one of the notes in the piece is modified, then an accidental is placed, which affects only within the bar. If the note reverts to its original position within the bar, then the natural symbol is placed before the note. See page 31.

NOTES FOR SINGERS

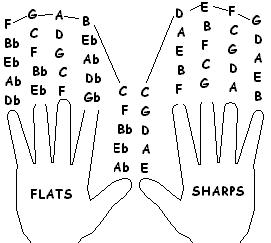Please sing the new note names. To find the Do of the new scale use the diagram on the left. Your Current Tonic is on the thumb, and the new Tonic is on the little finger. With each succeeding row, you get an additional sharp. First row from C to G. G is the Do of 1 sharp. The second row: G to D- D is the Do of 2 sharps. Third row: D to A - A is the Do of 3 sharps, and so on.

For flats use the left hand, and read the notes in the descending scale. C to F, this is the Do of 1 flat. F to Bb - Do of 2 flats. Bb to Eb - Do of 3 flats. Eb . to Ab - Do of 4 flats. Etc.

Remember, Mi is a third above Do, and La is third below it on so on. Remember rules learnt in Section 2. Soon you will be able to rename them with ease. You will get your p itch by association of the sound name. For Organ players use the English Alphabet name.

The starting note of the scale is called the Key note, or Tonic.

The fifth note is called Dominant

The fourth note is called the Subdominant.

The 3^rd is the Mediant, the 6^th is the sub mediant.

The 2^nd is the supertonic and the 7^th is the Leading note.

These are the names specific to harmony.

CHORDS OF THE DIFFERENT SCALES

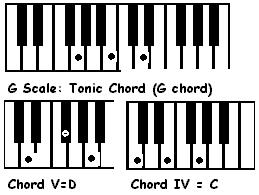
In every scale, the first, Tonic, the fourth Subdominant, and the fifth, Dominant are roots of Primary Major Chords.

The second, Supertonic, the third, Mediant and the sixth Sub mediant are minor chords. A suffix 'm' has to be written after the note name.

The seventh (Leading Note) is always a diminished chord.

The distance from the first note, called the ROOT to the third name above it, which is called the THIRD ABOVE THE ROOT has five chromatic keys between them.

C, C#,D,D#,E

The distance from the middle note (which is a third above the root) to the top note (which is A FIFTH ABOVE THE ROOT (because it is the fifth name after the root) has 8 chromatic keys between them. (C,C#,D,D#,E,F,F#,G)

Major Thirds

Distance between a key and the third above it, having 5 chromatic keys between them is called A MANOR THIRD. When there are 4 keys, it is called a MINOR THIRD.

Perfect Fifths

Distance between a key and the fifth above it, having 8 chromatic keys between them is called A PERFECT FIFTH.

A Major Chord has a major third, and a perfect fifth above the root

A “Dominant seventh chord” is a Major chord, with a minor third above the fifth. This note is seventh from the root. Such a 7^th having 11 chromatic keys between the root and the seventh is called a minor seventh. A major seventh has 12 keys, like C to B.

CHORDS OF THE MAJOR SCALE:

The Chords over the Tonic, Dominant and Subdominant are all Major Chords.

The Dominant Seventh has an additional 4^th note, which is a minor 7^th from the root.

The Minor Chords

The Chords of the Supertonic, Mediant and Submediant are Minor chords.

The Chord of the Leading Note is Diminished.

Explanation:

The Minor Chords of the C Scale:

Super Tonic: - 2^nd note of a scale.

Mediant – the 3^rd note of a scale.

Submediant – 6^th note of a scale.

The third above the root has 4 chromatic keys between them, hence a minor third.

The fifth above the root has 8 chromatic keys between them, hence is a perfect fifth.

A Minor Chord, has a minor third, and a perfect fifth above the root.

The Chord of the Leading Note:

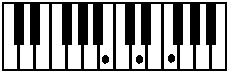
The third above the root is a minor third.

The fifth name above the root, has in this case only 7 keys between them, hence this fifth is called a diminished fifth.

A Diminished Chord

A chord having a minor third and a diminished fifth above the root is called a diminished chord.

In a transposed scale, i.e. having sharps and flats, and tonics other than C, (as given in the above lists), follow the above patterns. That is why in every scale, whether it be the Natural Scale of C, or the sharps and flats scales, the harmony names are common. They always have the first chord as the tonic, the chord on the fourth note is the subdominant, etc.

Chords of the G Scale.